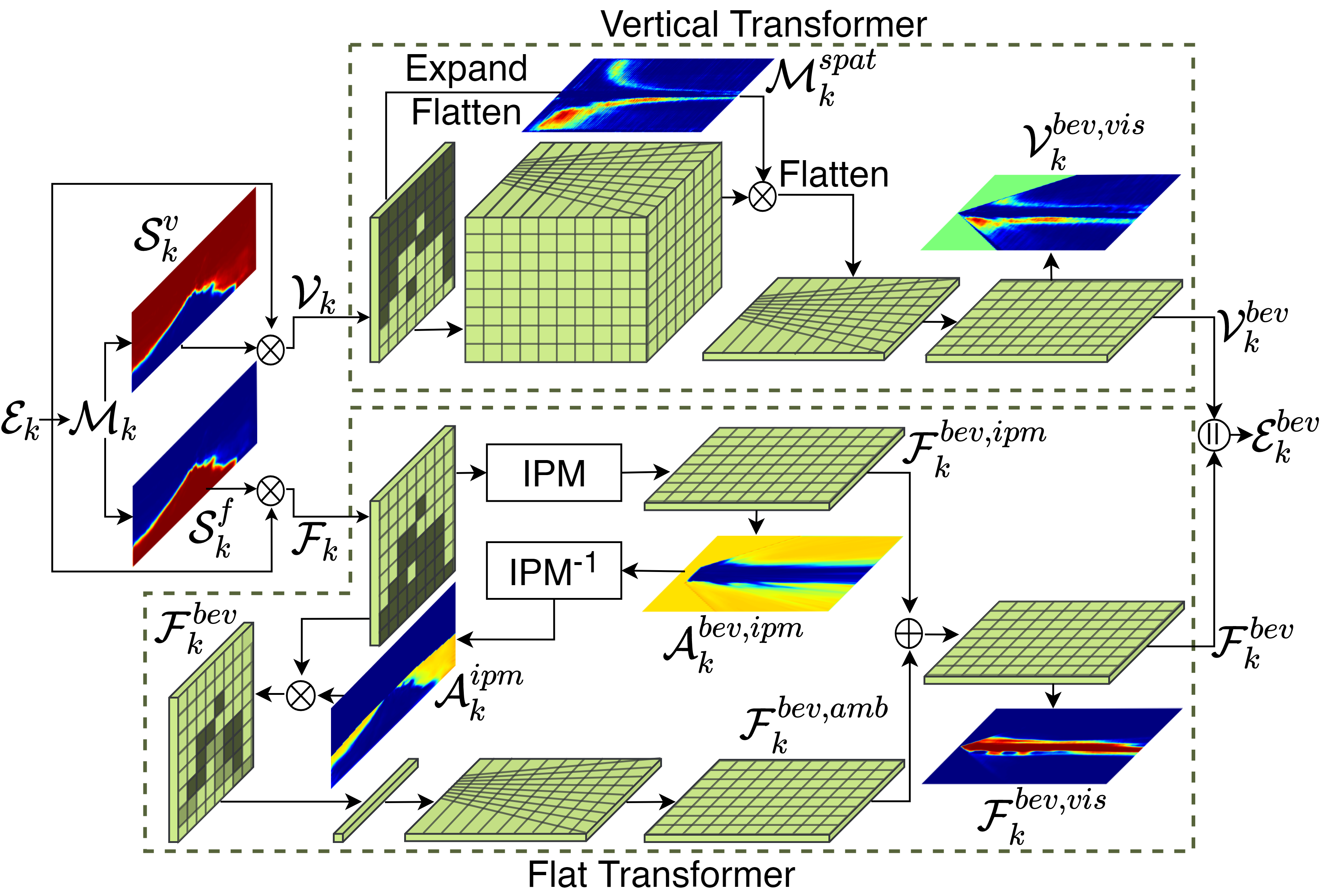
The design of our dense transformer module is based on the principle of how different regions in the 3D world are projected onto a perspective 2D image. Specifically, a column belonging to a flat region in the FV image projects onto a perspectively distorted area in the BEV, whereas a column belonging to a vertical non-flat region maps to an orthographic projection of a volumetric region in the BEV space. Accordingly, we employ two distinct transformers in our dense transformer module to independently map features from the vertical and flat regions in the FV to the BEV. Reflecting our observation, the vertical transformer expands the FV features into a volumetric lattice to model the intermediate 3D space before flattening it along the height dimension to generate the vertical BEV features. Parallelly, the flat transformer uses the IPM algorithm followed by our Error Correction Module to map the flat FV features into the BEV. The transformed vertical and flat features are then merged in the BEV space to generate the composite BEV feature map.
PanopticBEV Examples
A Neural Network-Based Approach to Generate Bird's-Eye-View Panoptic Segmentation Maps Using Frontal-View Monocular Images
These examples demonstrate the performance of our PanopticBEV model on the KITTI-360 and nuScenes datasets. PanopticBEV is the first end-to-end learning approach for directly generating dense panoptic segmentation maps in the bird's eye view given monocular images in the frontal view. To learn more about our work, please see the Technical Approach section. View the demo by selecting a dataset from the drop down box below and click on an image to view the predicted BEV panoptic segmentation map.
If you are unable to view the images for the KITTI-360 and nuScenes datasets below, please disable your AdBlocker and refresh the page.
Technical Approach
What are Bird's-Eye-View Maps?

Bird's-Eye-View (BEV) maps portray the scene around an autonomous vehicle as if it were viewed by a bird overflying the autonomous vehicle. Such representations provide rich spatial context and are extremely easy to interpret and process. They also capture absolute distances in the metric scale which allow them to be readily deployed in applications such as trajectory generation, path planning, and behaviour prediction, where a holistic view around an autonomous vehicle as well as the distance to nearby obstacles is essential.
Traditionally, BEV maps are created using complex multi-stage paradigms that encapsulate a series of distinct tasks such as depth estimation, semantic segmentation, and ground plane estimation. These tasks are often learned in a disjoint manner which prevents the model from holistic reasoning and results in erroneous BEV maps. Further, existing algorithms only predict semantics in the BEV space, which restricts their use in applications where the knowledge of object instances is crucial. To address these aforementioned challenges, we present the first end-to-end learning approach to directly generate a dense panoptic segmentation map in the BEV, given a monocular image in the frontal view (FV). We incorporate several key advances such as the dense transformer module and the sensitivity-based weighting function into our PanopticBEV architecture, which improves its performance as well as its efficiency.
PanopticBEV Architecture
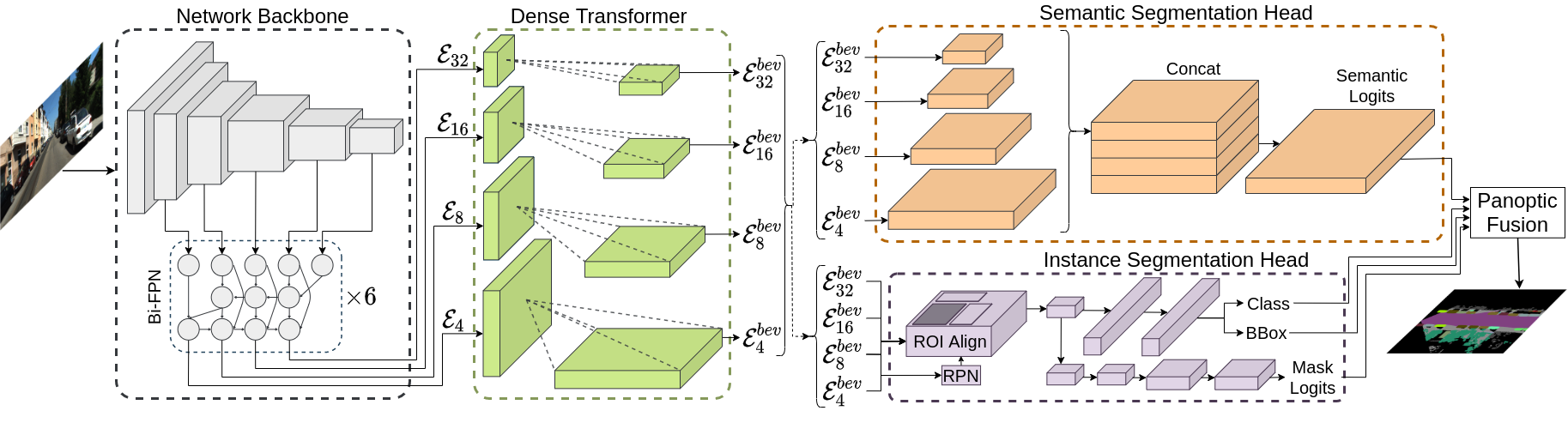
The goal of our PanopticBEV architecture is to generate a coherent panoptic segmentation mask in the BEV given a single monocular image in the FV. Our PanopticBEV model follows the top-down paradigm and is composed of a shared backbone, a dense transformer module, a semantic head, an instance head, and a panoptic fusion module. A custom variant of the EfficientDet-D3 backbone, adapted to work on larger feature maps, forms the backbone of our network and outputs feature maps of four scales \(\mathcal{E}_{4}, \mathcal{E}_{8}, \mathcal{E}_{16}, \mathcal{E}_{32} \). Each feature map is then transformed into the BEV using our dense transformer module, which consists of two distinct transformers to independently map the vertical and flat regions in the input FV image to the BEV. The transformed feature maps are then consumed by the EfficientPS-based semantic head and Mask-RCNN-based instance head to parallelly generate the semantic logits and instance masks. The semantics logits and instance masks are subsequently fused in the panoptic fusion module to generate the final BEV panoptic segmentation output.
Dense Transformer Module
Sensitivity-Based Weighting
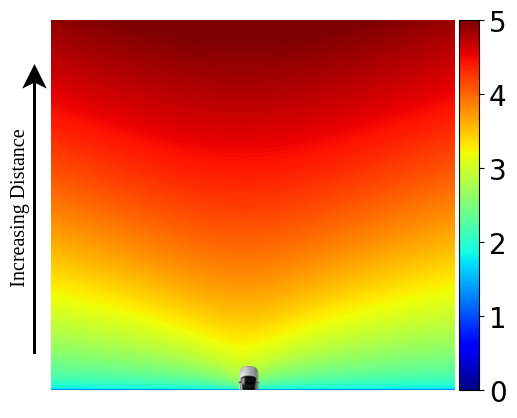
The sensitivity-based weighting function accounts for the varying levels of descriptiveness across the input FV image by intelligently weighting pixels in the BEV space. Owing to the perspective projection, the apparent motion in the input FV image for close regions is much larger than that of farther ones when a point in the 3D world is moved by a unit distance. This disparity makes differentiating between small changes in distance much more difficult for farther regions as compared to closer ones, resulting in high uncertainty in the distant regions. We address this problem by proposing a sensitivity-based weighting function to up-weight pixels belonging to far-away regions. This up-weighting allows the network to focus on the distant regions which improves the overall model accuracy. The sensitivity-based weighting function is defined as \[ S = \frac{\sqrt{f_x^2 z^2 + (f_x x + f_y y)^2}}{z^2} \qquad w_{sens} = 1 + \frac{1}{log(1 + \lambda_s S)} \] where \( f_x, f_y \) denote the focal length of the camera in terms of pixels, \( x, y, z \) represent the 3D position of the point of interest, and \( \lambda_s \) is a user-defined constant.
Bird's-Eye-View Panoptic Segmentation Datasets


We introduce two new BEV panoptic segmentation datasets for autonomous driving, namely, KITTI-360 PanopticBEV and nuScenes PanopticBEV that provides panoptic BEV ground truths for the KITTI-360 and nuScenes datasets respectively. KITTI-360 PanopticBEV consists of 9 scenes with a total of 64071 FV-BEV image pairs, while the nuScenes PanopticBEV dataset consists of a total of 850 scenes with a total of 34149 FV-BEV image pairs. We provide annotations for 7 'stuff' and 4 'thing' classes for the KITTI-360 PanopticBEV dataset, and annotations for 6 'stuff' and 4 'thing' classes for the nuScenes PanopticBEV dataset. We also publicly release the code used to generate the BEV datasets to promote FV-BEV image pair creation for other large-scale urban datasets.
License Agreement
Videos
Publications
Nikhil Gosala,
Abhinav Valada,
"Bird's-Eye-View Panoptic Segmentation Using Monocular Frontal View Images",
IEEE Robotics and Automation Letters (RA-L), 2022.
People
Acknowledgement
This work was funded by the Eva Mayr-Stihl Stiftung and the Federal Ministry of Education and Research (BMBF) of Germany under ISA 4.0.


